• Rozwiązania:
• Zadanie 1
• Zadanie 2
• Zadanie 3
• Zadanie 4
• Zadanie 5
• Zadanie 6

Elektronika analogowa - tranzystor bipolarny

Zadanie 1: Dla układu jak na poniższym schemacie (gdzie V_CC = 10 V, R_C = 3 kΩ,
R_B = 1.86 MΩ, β = 200) wyznaczyć punkt pracy (I_C, V_CE) oraz policzyć wzmocnienie
napięciowe (K_V) i wyznaczyć rezystancję wejściową (r_we).

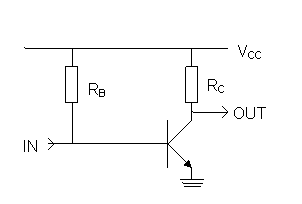
Rozwiązanie:

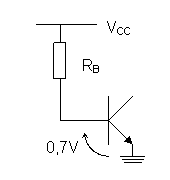Analizując fragment układu z rysunku obok możemy z prawa Kirchoffa napisać równanie:

V_CC = I_BR_B + 0,7

Zatem:

Podstawiając:   

I_C = β · I_B, zatem: I_C = 200 · 5μA = 1 mA.

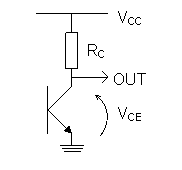
Analizując fragment układu z rysunku obok możemy z prawa Kirchoffa napisać równanie:

V_CC = I_CR_C + V_CE

Zatem szukane napięcie V_CE:

V_CE = V_CC - I_CR_C

Podstawiając dane: V_CE = 10 V - 3 kΩ · 1 mA = 10 V - 3 V = 7 V.

Schemat małosygnałowy

Aby obliczyć K_V i r_we posłużymy się schematem małosygnałowym naszego układu:

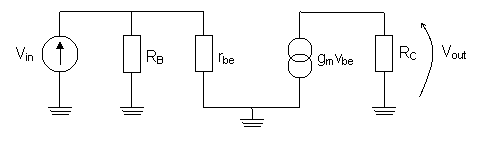
Na schemacie małosygnałowym mamy dodatkowe parametry: V_be i g_m.

,

.

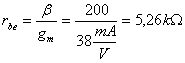Ze schematu widać, że napięcie wejściowe jest równe napięciu odłożonemu na r_be:

V_IN = V_be,

zaś napięcie wyjściowe, to napięcie odłożone na rezystorze R_C, które możemy policzyć z prawa Ohma, jako iloczyn oporności R_C i przepływającego przez nią prądu (który w naszym przypadku jest prądem ze źródła prądowego):

V_OUT = - R_C · g_mV_be.

Zatem szukane wzmocnienie napięciowe K_V wyraża się wzorem:

.

Szukając rezystancji wejściowej określamy zastępczą rezystancję od wejścia do masy, co w naszym przypadku jest równoległym połączeniem R_B i r_be:

r_we = R_B || r_be,

Ponieważ R_B = 1.86 MΩ, a r_be = 5,26 kΩ, zatem równoległe połączenie tych dwóch rezystancji da rezystancję zastępczą bliską mniejszej z nich, zatem:

r_we = r_be = 5,26 kΩ.

© copyright kluza